Referencia: Oppenheim 4.1. p285, Lathi 7.2 p680
El planteamiento de Fourier es que una señal aperiódica (no periódica) puede observarse como una señal periódica con periodo infinito.
[ exponencial decreciente ] [ exponencial decreciente con |t| ] [ rectangular ] [ Pulso unitario ]
…
Ejercicio 1. exponencial decreciente con μ(t)
Referencia: Oppenheim Ejercicio 4.1 p290, Lathi ejemplo 7.1 p685, Hsu Ejemplo 5.2 p218
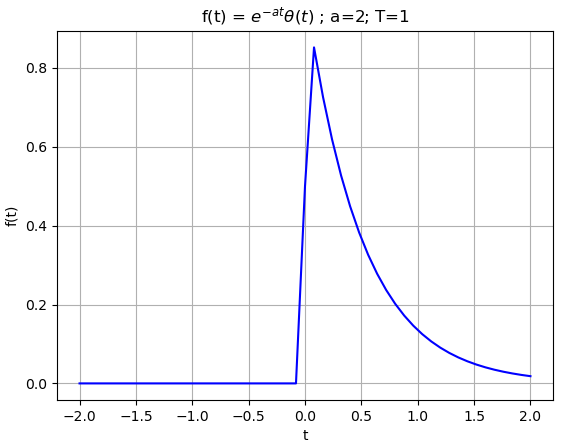
Considere la señal contínua exponencial decreciente, desarrolle la transformada de Fourier
x(t) =e^{-at} \mu (t) \text{ ; } a \gt 0el integral a desarrollar,
X(\omega) =\int_{-\infty}^{\infty} e^{-at} \mu (t) e^{-j \omega t} \delta t X(\omega) =\int_{0}^{\infty} e^{-(a+j\omega)t} \delta t =-\frac{1}{a+j\omega} e^{-(a+j\omega)t} \Big|_{0}^{\infty} X(\omega) =-\frac{1}{a+j\omega} e^{-(a+j\omega)(\infty)} +\frac{1}{a+j\omega} e^{-(a+j\omega)(0)} X(\omega) = \frac{1}{a+j\omega}para a>0
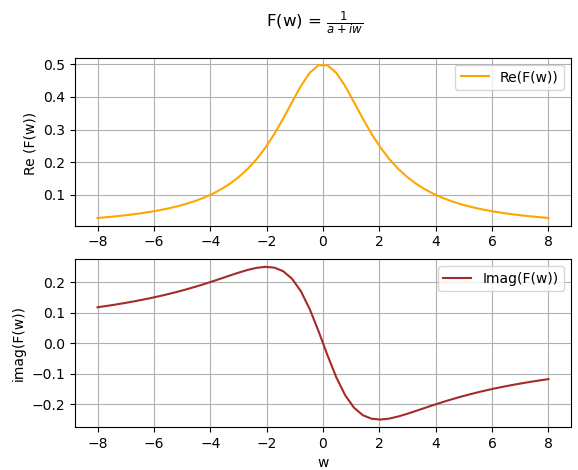
Se obtiene una parte real y otra imaginaria al evaluar F(w) en un intervalo que incluya -a y a.
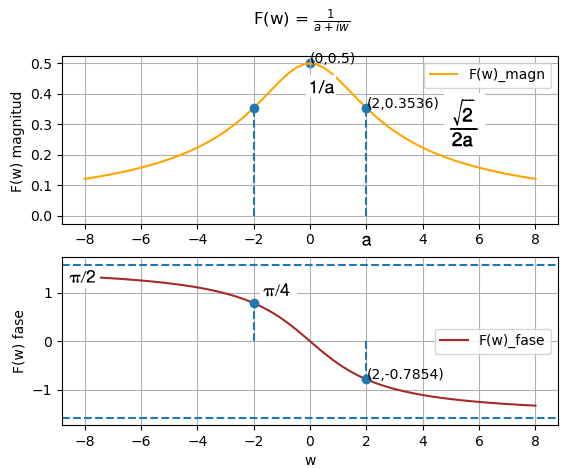
También es posible observar la magnitud y fase de F(w) en una gráfica.
Se observa por ejemplo que el valor de la magnitud |F(0)| = 1/a. También que la fase se encuentra acotada en π/2 y que fase(F(-a)) = -π/4.
Usando el algoritmo con Python se obtiene el siguiente resultado:
expresion f(t):
-a*t
e *Heaviside(t)
expresion F(w):
1
-------
a + I*w
|F(w)|:
1
------------
_________
/ 2 2
\/ a + w
F(w)_fase:
/w\
-atan|-|
\a/
>>>
Instrucciones en Python
# Transformada de Fourier de señales aperiodicas # blog.espol.edu.ec/telg1001/ import sympy as sym # INGRESO t = sym.Symbol('t', real=True,) w = sym.Symbol('w', real=True) a = sym.Symbol('a', real=True,positive=True) T = sym.Symbol('T', real=True,positive=True) j = sym.I u = sym.Heaviside(t) d = sym.DiracDelta(t) ft = sym.exp(-a*t)*u #ft = sym.exp(-a*sym.Abs(t)) #ft = sym.Heaviside(t+T)-sym.Heaviside(t-T) #ft = d # PROCEDIMIENTO unilateral = False ftw = ft*sym.exp(-j*w*t) # f(t,w) para integrar ftw = sym.expand(ftw) # expresion de sumas ftw = sym.powsimp(ftw) # simplifica exponentes lim_a = 0 # unilateral if not(unilateral): lim_a = -sym.oo # integral de Fourier Fw_F = sym.integrate(ftw,(t,lim_a,sym.oo)) if Fw_F.is_Piecewise: Fw = Fw_F.args[0] # primera ecuacion e intervalo Fw = Fw[0] # solo expresion else: Fw = Fw_F Fw = Fw.simplify() # Magnitud y Fase Fw_magn = sym.Abs(Fw) Fw_fase = sym.atan(sym.im(Fw)/sym.re(Fw)) # SALIDA print('\n expresion f(t):') sym.pprint(ft) print('\n expresion F(w):') sym.pprint(Fw) print('\n |F(w)|:') sym.pprint(Fw_magn) print('\n F(w)_fase:') sym.pprint(Fw_fase)
Instrucción simplificada con Sympy
La librería Sympy incorpora una función para determinar en forma simbólica la transformada de Fourier, se usa la instrucción para simplificar el algoritmo anterior.
# Transformada de Fourier de señales aperiodicas # blog.espol.edu.ec/telg1001/ import sympy as sym # INGRESO t = sym.Symbol('t', real=True,) w = sym.Symbol('w', real=True) a = sym.Symbol('a', real=True,positive=True) T = sym.Symbol('T', real=True,positive=True) j = sym.I u = sym.Heaviside(t) d = sym.DiracDelta(t) ft = sym.exp(-a*t)*u #ft = sym.exp(-a*sym.Abs(t)) #ft = u.subs(t,t+T)-u.subs(t,t-T) #ft = d # PROCEDIMIENTO ft = sym.expand(ft) # expresion de sumas Fw = sym.fourier_transform(ft,t,w/(2*sym.pi)) # Magnitud y Fase Fw_magn = sym.Abs(Fw) Fw_fase = sym.atan(sym.im(Fw)/sym.re(Fw)) # SALIDA print('\n expresion f(t):') sym.pprint(ft) print('\n expresion F(w):') sym.pprint(Fw) print('\n |F(w)|:') sym.pprint(Fw_magn) print('\n F(w)_fase:') sym.pprint(Fw_fase)
Instrucciones para añadir la gráfica
Para las gráficas, se dan valores a las constantes a, T, se define el intervalo de la gráfica y el número de muestras a usar.
Luego se sustituye en las ecuaciones resultantes los valores de ‘a‘ con ‘a_k‘ obteniendo valores para las gráficas. La gráfica para f(t) se realiza de forma semejante en la unidad 1. Para la gráfica F(w) se usan una gráfica con parte Real e Imaginaria, otra gráfica para magnitud y fase.
# GRAFICA ---------------- import numpy as np import matplotlib.pyplot as plt import telg1001 as fcnm equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] a_k = 2 # valor de 'a' constante # Grafica, intervalo tiempo [t_a,t_b] T_k = 1 # valor T o periodo t_a = -2*T_k ; t_b = 2*T_k muestras = 52 # 51 resolucion grafica ft = ft.subs({a:a_k,T:T_k}) # a tiene valor a_k Fw = Fw.subs({a:a_k,T:T_k}) Fw_magn = Fw_magn.subs({a:a_k,T:T_k}) Fw_fase = Fw_fase.subs({a:a_k,T:T_k}) figura_ft = fcnm.graficar_ft(ft,t_a,t_b,muestras) # F(w) real e imaginaria w_a = -a_k*4 ; w_b = a_k*4 wi = np.linspace(w_a,w_b,muestras) # convierte a sympy una constante Fw = sym.sympify(Fw,w) if Fw.has(w): # no es constante F_w = sym.lambdify(w,Fw, modules=equivalentes) else: F_w = lambda w: Fw + 0*w Fwi = F_w(wi) # evalua wi # F(w) magnitud y fase # convierte a sympy una constante Fw_magn = sym.sympify(Fw_magn,w) if Fw_magn.has(w): # no es constante F_w_magn = sym.lambdify(w,Fw_magn, modules=equivalentes) else: F_w_magn = lambda w: Fw_magn + 0*w # convierte a sympy una constante Fw_fase = sym.sympify(Fw_fase,w) if Fw_fase.has(w): # no es constante F_w_fase = sym.lambdify(w,Fw_fase, modules=equivalentes) else: F_w_fase = lambda w: Fw_fase + 0*w Fwi_magn = F_w_magn(wi) # evalua wi Fwi_fase = F_w_fase(wi) # F(w) real e imaginaria fig_Fw, graf_Fwi = plt.subplots(2,1) graf_Fwi[0].plot(wi,np.real(Fwi),label='Re(F(w))', color='orange') graf_Fwi[0].legend() graf_Fwi[0].set_ylabel('Re (F(w)) ') graf_Fwi[0].grid() graf_Fwi[1].plot(wi,np.imag(Fwi),label='Imag(F(w))', color='brown') graf_Fwi[1].legend() graf_Fwi[1].set_xlabel('w') graf_Fwi[1].set_ylabel('imag(F(w))') graf_Fwi[1].grid() plt.suptitle(r'F(w) = $'+str(sym.latex(Fw))+'$') # plt.show() # F(w) magnitud y fase fig_Fwmg, graf_Fw = plt.subplots(2,1) graf_Fw[0].plot(wi,Fwi_magn,label='F(w)_magn', color='orange') Fwa0 = F_w_magn(0) Fwa1 = F_w_magn(-a_k) Fwa2 = F_w_magn(a_k) if Fw_magn.has(w): # no es constante graf_Fw[0].stem([-a_k,a_k],[Fwa1,Fwa2], basefmt=' ',linefmt ='--') etiqueta1 = '('+str(a_k)+','+str(round(Fwa2,4))+')' graf_Fw[0].annotate(etiqueta1, xy=(a_k,Fwa2)) etiqueta0 = '('+str(0)+','+str(round(Fwa0,4))+')' graf_Fw[0].scatter(0,Fwa0) graf_Fw[0].annotate(etiqueta0, xy=(0,Fwa0)) graf_Fw[0].legend() graf_Fw[0].set_ylabel('F(w) magnitud ') graf_Fw[0].grid() graf_Fw[1].plot(wi,Fwi_fase,label='F(w)_fase', color='brown') graf_Fw[1].axhline(np.pi/2,linestyle ='--') graf_Fw[1].axhline(-np.pi/2,linestyle ='--') if Fw_magn.has(w): # no es constante Fwa1f = F_w_fase(-a_k) Fwa2f = F_w_fase(a_k) graf_Fw[1].stem([-a_k,a_k],[Fwa1f,Fwa2f], basefmt=' ',linefmt ='--') etiqueta3 = '('+str(a_k)+','+str(round(Fwa2f,4))+')' graf_Fw[1].annotate(etiqueta3, xy=(a_k,Fwa2f)) graf_Fw[1].legend() graf_Fw[1].set_xlabel('w') graf_Fw[1].set_ylabel('F(w) fase') graf_Fw[1].grid() plt.suptitle(r'F(w) = $'+str(sym.latex(Fw))+'$') plt.show()
[ exponencial decreciente ] [ exponencial decreciente con |t| ] [ rectangular ] [ Pulso unitario ]
…
Ejercicio 2. exponencial decreciente con |t|, función par
Referencia: Oppenheim Ejercicio 4.2 p291, Lathi ejemplo 7. p685, Hsu 5.21 p248
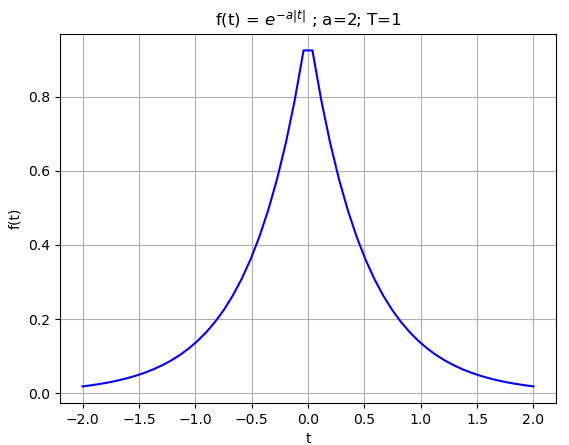
Considere la señal contínua exponencial decreciente, desarrolle la transformada de Fourier
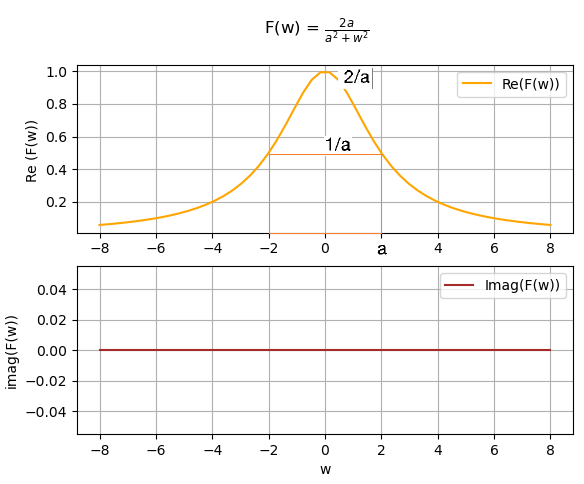
x(t) =e^{-a|t|} \text{ ; } a \gt 0 X(\omega) = \int_{-\infty}^{\infty}e^{-a|t|} e^{-j \omega t} \delta t X(\omega) = \int_{-\infty}^{0}e^{at} e^{-j \omega t} \delta t + \int_{0}^{\infty}e^{-at} e^{-j \omega t} \delta t = \int_{-\infty}^{0}e^{at-j \omega t} \delta t + \int_{0}^{\infty}e^{-at-j \omega t} \delta t = \frac{1}{at-j \omega} e^{(a-j \omega) t}\Big|_{-\infty}^{0} - \frac{1}{a+j\omega}e^{-(at+j \omega) t} \Big| _{0}^{\infty} = \Big[ \frac{1}{at-j \omega} e^{(a-j \omega) (0)} - \frac{1}{at-j \omega t} e^{(a-j \omega) (-\infty)} \Big] + - \Big[ \frac{1}{a+j\omega}e^{-(at+j \omega) (\infty)} - \frac{1}{a+j\omega}e^{-(at+j \omega)(0)}\Big] = \frac{1}{a-j\omega} +\frac{1}{a+j\omega} = \frac{a+j\omega+ a-j\omega}{(a-j\omega)(a+j\omega)} X(\omega) = \frac{2a}{(a^2+\omega^2)}Para desarrollar el ejercicio con el algoritmo, la entrada de señal se expresaría en el algoritmo como:
ft = sym.exp(-a*sym.Abs(t)) # Ej 4.2 Oppenheim
el resultado a comparar con el desarrollo analítico es:
expresion f(t): -a*|t| e expresion F(w): 2*a ------- 2 2 a + w |F(w)|: 2*a ------- 2 2 a + w F(w)_fase: 0
Grafica de F(w) magnitud y fase
El algoritmo es el mismo que el ejercicio 1, modificando el bloque de ingreso para el problema
[ exponencial decreciente ] [ exponencial decreciente con |t| ] [ rectangular ] [ Pulso unitario ]
…
Ejercicio 3. Rectangular centrada en origen
Referencia: Oppenheim Ejercicio 4.4 p293, Lathi ejemplo 7.2 p689, Hsu 5.19 p247
Considere la señal pulso rectangular o pulso compuerta (gate), desarrolle la transformada de Fourier
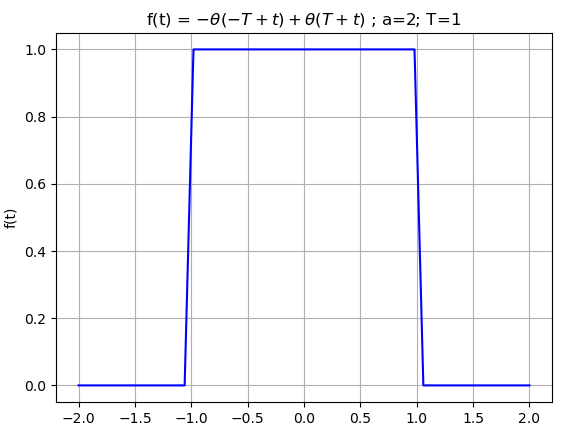
x(t) =\begin{cases}1 && |t|<T_1, \\ 0 && |t|>T_1\end{cases} X(\omega) = \int_{-T_1}^{T_1} e^{-j\omega t} \delta t = -\frac{1}{j \omega} e^{-j\omega t}\Big|_{-T_1}^{T_1} = -\frac{1}{j \omega} \Big[ e^{-j\omega (T_1)} - e^{-j\omega (-T_1)}\Big] = -\frac{1}{j \omega} \Big[ e^{-T_1 j\omega } - e^{jT_1\omega } \Big] = \frac{1}{j \omega} e^{T_1 j\omega} - \frac{1}{j \omega} e^{-T_1 j\omega }en este punto es conveniente usar la forma trigonometrica de un exponencial con exponente complejo
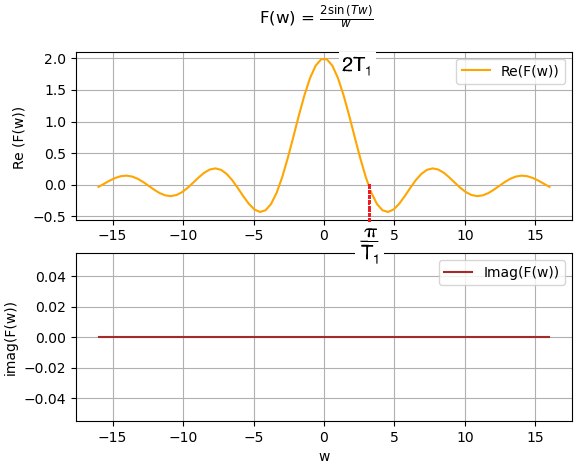
= \frac{1}{j \omega} (\cos (T_1\omega)+j \sin(T_1\omega)) - \frac{1}{j \omega} (cos(T_1 \omega) -jsin(T_1\omega)) = \frac{1}{j \omega}\cos (T_1\omega)+j\frac{1}{j \omega} \sin(T_1\omega) - \frac{1}{j \omega} cos(T_1 \omega) +j\frac{1}{j \omega} sin(T_1\omega)) X(\omega) = 2\frac{\sin(T_1\omega)}{\omega}Para desarrollar el ejercicio con el algoritmo, la señal se expresaría como:
ft = sym.Heaviside(t+T)-sym.Heaviside(t-T) # Ej 4.4 Oppenheim
obteniendo el siguiente resultado
expresion f(t):
-Heaviside(-T + t) + Heaviside(T + t)
expresion F(w):
2*sin(T*w)
----------
w
|F(w)|:
|sin(T*w)|
2*|--------|
| w |
F(w)_fase:
0
con la siguiente gráfica f(T)
gráfica de F(w) parte real e imaginaria
El algoritmo es el mismo que el ejercicio 1, modificando el bloque de ingreso para el problema
[ exponencial decreciente ] [ exponencial decreciente con |t| ] [ rectangular ] [ Pulso unitario ]
…
Ejercicio 4. Pulso unitario
Referencia: Oppenheim Ejercicio 4.3 p292, Lathi ejemplo 7.3 p693, Hsu 5.1 p218
Considere la señal pulso unitario, desarrolle la transformada de Fourier
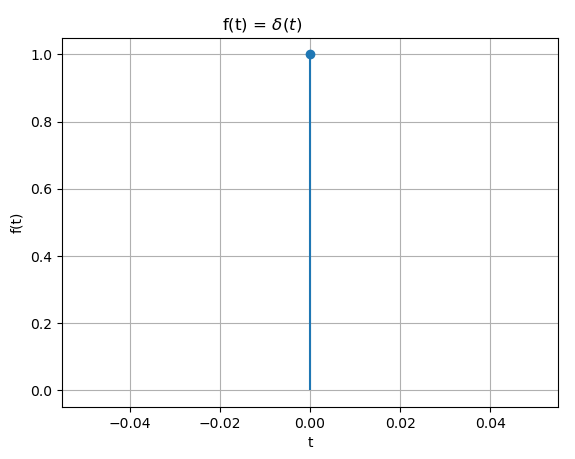
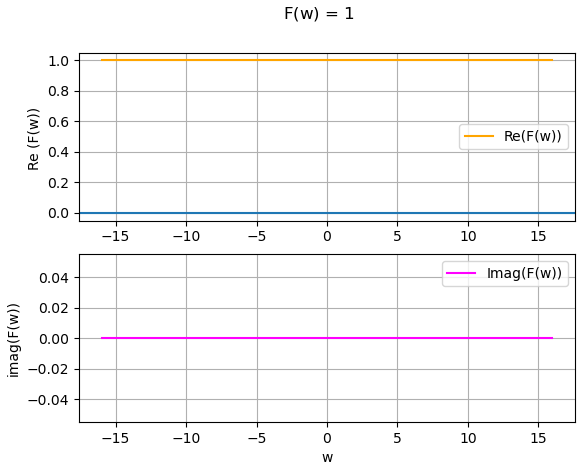
x(t) = \delta (t) X(j\omega) = \int_{-\infty}^{\infty} \delta (t) e^{-j \omega t} \delta t = 1Es decir la transformada de Fourier tiene componentes de todas las frecuencias.
El algoritmo entrega el siguiente resultado:
expresion f(t): DiracDelta(t) expresion F(w): 1 |F(w)|: 1 F(w)_fase: 0
El pulso unitario se define en Sympy como:
ft = sym.DiracDelta(t) # Ej 4.3 Oppenheim
En la parte gráfica, el pulsos unitarios se grafican con plt.stem(0,1), no requiriendo el resto de las graficas para observar el resultado.
El algoritmo es el mismo que el ejercicio 1, modificando el bloque de ingreso para el problema
Tarea: Realizar otros ejercicios con exponenciales para comprobar la operación del algoritmo.
[ exponencial decreciente ] [ exponencial decreciente con |t| ] [ rectangular ] [ Pulso unitario ]